Function (Snowflake)

Note

Please always keep the schema name SEDONA (e.g., SEDONA.ST_GeomFromWKT) when you use Sedona functions to avoid conflicting with Snowflake's built-in functions.

GeometryType

Introduction: Returns the type of the geometry as a string. Eg: 'LINESTRING', 'POLYGON', 'MULTIPOINT', etc. This function also indicates if the geometry is measured, by returning a string of the form 'POINTM'.

Format: GeometryType (A: Geometry)

SQL Example:

SELECT GeometryType(ST_GeomFromText('LINESTRING(77.29 29.07,77.42 29.26,77.27 29.31,77.29 29.07)'));

Output:

 geometrytype
--------------
 LINESTRING

SELECT GeometryType(ST_GeomFromText('POINTM(0 0 1)'));

Output:

 geometrytype
--------------
 POINTM

ST_3DDistance

Introduction: Return the 3-dimensional minimum cartesian distance between A and B

Format: ST_3DDistance (A:geometry, B:geometry)

SQL example:

SELECT ST_3DDistance(polygondf.countyshape, polygondf.countyshape)
FROM polygondf

ST_AddPoint

Introduction: RETURN Linestring with additional point at the given index, if position is not available the point will be added at the end of line.

Format: ST_AddPoint(geom: geometry, point: geometry, position: integer)

Format: ST_AddPoint(geom: geometry, point: geometry)

SQL example:

SELECT ST_AddPoint(ST_GeomFromText('LINESTRING(0 0, 1 1, 1 0)'), ST_GeomFromText('Point(21 52)'), 1)

SELECT ST_AddPoint(ST_GeomFromText('Linestring(0 0, 1 1, 1 0)'), ST_GeomFromText('Point(21 52)'))

Output:

LINESTRING(0 0, 21 52, 1 1, 1 0)
LINESTRING(0 0, 1 1, 1 0, 21 52)

ST_Affine

Introduction: Apply an affine transformation to the given geometry.

ST_Affine has 2 overloaded signatures:

ST_Affine(geometry, a, b, c, d, e, f, g, h, i, xOff, yOff, zOff)

ST_Affine(geometry, a, b, d, e, xOff, yOff)

Based on the invoked function, the following transformation is applied:

x = a * x + b * y + c * z + xOff OR x = a * x + b * y + xOff

y = d * x + e * y + f * z + yOff OR y = d * x + e * y + yOff

z = g * x + f * y + i * z + zOff OR z = g * x + f * y + zOff

If the given geometry is empty, the result is also empty.

Format:

ST_Affine(geometry, a, b, c, d, e, f, g, h, i, xOff, yOff, zOff)

ST_Affine(geometry, a, b, d, e, xOff, yOff)

ST_Affine(geometry, 1, 2, 4, 1, 1, 2, 3, 2, 5, 4, 8, 3)

Input: LINESTRING EMPTY

Output: LINESTRING EMPTY

Input: POLYGON ((1 0 1, 1 1 1, 2 2 2, 1 0 1))

Output: POLYGON Z((9 11 11, 11 12 13, 18 16 23, 9 11 11))

Input: POLYGON ((1 0, 1 1, 2 1, 2 0, 1 0), (1 0.5, 1 0.75, 1.5 0.75, 1.5 0.5, 1 0.5))

Output: POLYGON((5 9, 7 10, 8 11, 6 10, 5 9), (6 9.5, 6.5 9.75, 7 10.25, 6.5 10, 6 9.5))

ST_Affine(geometry, 1, 2, 1, 2, 1, 2)

Input: POLYGON EMPTY

Output: POLYGON EMPTY

Input: GEOMETRYCOLLECTION (MULTIPOLYGON (((1 0, 1 1, 2 1, 2 0, 1 0), (1 0.5, 1 0.75, 1.5 0.75, 1.5 0.5, 1 0.5)), ((5 0, 5 5, 7 5, 7 0, 5 0))), POINT (10 10))

Output: GEOMETRYCOLLECTION (MULTIPOLYGON (((2 3, 4 5, 5 6, 3 4, 2 3), (3 4, 3.5 4.5, 4 5, 3.5 4.5, 3 4)), ((6 7, 16 17, 18 19, 8 9, 6 7))), POINT (31 32))

Input: POLYGON ((1 0 1, 1 1 1, 2 2 2, 1 0 1))

Output: POLYGON Z((2 3 1, 4 5 1, 7 8 2, 2 3 1))

ST_Angle

Introduction: Computes and returns the angle between two vectors represented by the provided points or linestrings.

There are three variants possible for ST_Angle:

ST_Angle(point1: Geometry, point2: Geometry, point3: Geometry, point4: Geometry) Computes the angle formed by vectors represented by point1 - point2 and point3 - point4

ST_Angle(point1: Geometry, point2: Geometry, point3: Geometry) Computes the angle formed by vectors represented by point2 - point1 and point2 - point3

ST_Angle(line1: Geometry, line2: Geometry) Computes the angle formed by vectors S1 - E1 and S2 - E2, where S and E denote start and end points respectively

Note

If any other geometry type is provided, ST_Angle throws an IllegalArgumentException.

Additionally, if any of the provided geometry is empty, ST_Angle throws an IllegalArgumentException.

Note

If a 3D geometry is provided, ST_Angle computes the angle ignoring the z ordinate, equivalent to calling ST_Angle for corresponding 2D geometries.

Tip

ST_Angle returns the angle in radian between 0 and 2\Pi. To convert the angle to degrees, use ST_Degrees.

Format: ST_Angle(p1, p2, p3, p4) | ST_Angle(p1, p2, p3) | ST_Angle(line1, line2)

SQL Example:

SELECT ST_Angle(ST_GeomFromWKT('POINT(0 0)'), ST_GeomFromWKT('POINT (1 1)'), ST_GeomFromWKT('POINT(1 0)'), ST_GeomFromWKT('POINT(6 2)'))

Output:

0.4048917862850834

SQL Example:

SELECT ST_Angle(ST_GeomFromWKT('POINT (1 1)'), ST_GeomFromWKT('POINT (0 0)'), ST_GeomFromWKT('POINT(3 2)'))

Output:

0.19739555984988044

SQL Example:

SELECT ST_Angle(ST_GeomFromWKT('LINESTRING (0 0, 1 1)'), ST_GeomFromWKT('LINESTRING (0 0, 3 2)'))

Output:

0.19739555984988044

ST_Area

Introduction: Return the area of A

Format: ST_Area (A:geometry)

SQL example:

SELECT ST_Area(polygondf.countyshape)
FROM polygondf

ST_AreaSpheroid

Introduction: Return the geodesic area of A using WGS84 spheroid. Unit is square meter. Works better for large geometries (country level) compared to ST_Area + ST_Transform. It is equivalent to PostGIS ST_Area(geography, use_spheroid=true) function and produces nearly identical results.

Geometry must be in EPSG:4326 (WGS84) projection and must be in lat/lon order. You can use ST_FlipCoordinates to swap lat and lon.

Format: ST_AreaSpheroid (A:geometry)

SQL example:

SELECT ST_AreaSpheroid(ST_GeomFromWKT('Polygon ((35 34, 30 28, 34 25, 35 34))'))

Output: 201824850811.76245

ST_AsBinary

Introduction: Return the Well-Known Binary representation of a geometry

Format: ST_AsBinary (A:geometry)

SQL example:

SELECT ST_AsBinary(polygondf.countyshape)
FROM polygondf

ST_AsEWKB

Introduction: Return the Extended Well-Known Binary representation of a geometry. EWKB is an extended version of WKB which includes the SRID of the geometry. The format originated in PostGIS but is supported by many GIS tools. If the geometry is lacking SRID a WKB format is produced. See ST_SetSRID

Format: ST_AsEWKB (A:geometry)

SQL example:

SELECT ST_AsEWKB(polygondf.countyshape)
FROM polygondf

ST_AsEWKT

Introduction: Return the Extended Well-Known Text representation of a geometry. EWKT is an extended version of WKT which includes the SRID of the geometry. The format originated in PostGIS but is supported by many GIS tools. If the geometry is lacking SRID a WKT format is produced. See ST_SetSRID

Format: ST_AsEWKT (A:geometry)

SQL example:

SELECT ST_AsEWKT(polygondf.countyshape)
FROM polygondf

ST_AsGeoJSON

Introduction: Return the GeoJSON string representation of a geometry

Format: ST_AsGeoJSON (A:geometry)

SQL example:

SELECT ST_AsGeoJSON(polygondf.countyshape)
FROM polygondf

ST_AsGML

Introduction: Return the GML string representation of a geometry

Format: ST_AsGML (A:geometry)

SQL example:

SELECT ST_AsGML(polygondf.countyshape)
FROM polygondf

ST_AsHEXEWKB

Introduction: This function returns the input geometry encoded to a text representation in HEXEWKB format. The HEXEWKB encoding can use either little-endian (NDR) or big-endian (XDR) byte ordering. If no encoding is explicitly specified, the function defaults to using the little-endian (NDR) format.

Format: ST_AsHEXEWKB(geom: Geometry, endian: String = NDR)

SQL Example

SELECT ST_AsHEXEWKB(ST_GeomFromWKT('POINT(1 2)'), 'XDR')

Output:

00000000013FF00000000000004000000000000000

SQL Example

SELECT ST_AsHEXEWKB(ST_GeomFromWKT('LINESTRING (30 20, 20 25, 20 15, 30 20)'))

Output:

0102000000040000000000000000003E4000000000000034400000000000003440000000000000394000000000000034400000000000002E400000000000003E400000000000003440

ST_AsKML

Introduction: Return the KML string representation of a geometry

Format: ST_AsKML (A:geometry)

SQL example:

SELECT ST_AsKML(polygondf.countyshape)
FROM polygondf

ST_AsText

Introduction: Return the Well-Known Text string representation of a geometry

Format: ST_AsText (A:geometry)

SQL example:

SELECT ST_AsText(polygondf.countyshape)
FROM polygondf

ST_Azimuth

Introduction: Returns Azimuth for two given points in radians null otherwise.

Format: ST_Azimuth(pointA: Point, pointB: Point)

SQL example:

SELECT ST_Azimuth(ST_POINT(0.0, 25.0), ST_POINT(0.0, 0.0))

Output: 3.141592653589793

ST_BestSRID

Introduction: Returns the estimated most appropriate Spatial Reference Identifier (SRID) for a given geometry, based on its spatial extent and location. It evaluates the geometry's bounding envelope and selects an SRID that optimally represents the geometry on the Earth's surface. The function prioritizes Universal Transverse Mercator (UTM), Lambert Azimuthal Equal Area (LAEA), or falls back to the Mercator projection. The function takes a WGS84 geometry and must be in lon/lat order.

• For geometries in the Arctic or Antarctic regions, the Lambert Azimuthal Equal Area projection is used.
• For geometries that fit within a single UTM zone and do not cross the International Date Line (IDL), a corresponding UTM SRID is chosen.
• In cases where none of the above conditions are met, the function defaults to the Mercator projection.
• For Geometries that cross the IDL, ST_BestSRID defaults the SRID to Mercator. Currently, ST_BestSRID does not handle geometries crossing the IDL.

Warning

ST_BestSRID is designed to estimate a suitable SRID from a set of approximately 125 EPSG codes and works best for geometries that fit within the UTM zones. It should not be solely relied upon to determine the most accurate SRID, especially for specialized or high-precision spatial requirements.

Format: ST_BestSRID(geom: Geometry)

Since: v1.6.0

SQL Example:

SELECT ST_BestSRID(ST_GeomFromWKT('POLYGON((-73.9980 40.7265, -73.9970 40.7265, -73.9970 40.7255, -73.9980 40.7255, -73.9980 40.7265))'))

Output:

32618

ST_Boundary

Introduction: Returns the closure of the combinatorial boundary of this Geometry.

Format: ST_Boundary(geom: geometry)

SQL example:

SELECT ST_Boundary(ST_GeomFromText('POLYGON((1 1,0 0, -1 1, 1 1))'))

Output: LINESTRING (1 1, 0 0, -1 1, 1 1)

ST_BoundingDiagonal

Introduction: Returns a linestring spanning minimum and maximum values of each dimension of the given geometry's coordinates as its start and end point respectively. If an empty geometry is provided, the returned LineString is also empty. If a single vertex (POINT) is provided, the returned LineString has both the start and end points same as the points coordinates

Format: ST_BoundingDiagonal(geom: Geometry)

SQL Example:

SELECT ST_BoundingDiagonal(ST_GeomFromWKT(geom))

Input: POLYGON ((1 1 1, 3 3 3, 0 1 4, 4 4 0, 1 1 1))

Output: LINESTRING Z(0 1 1, 4 4 4)

Input: POINT (10 10)

Output: LINESTRING (10 10, 10 10)

Input: GEOMETRYCOLLECTION(POLYGON ((5 5 5, -1 2 3, -1 -1 0, 5 5 5)), POINT (10 3 3))

Output: LINESTRING Z(-1 -1 0, 10 5 5)

ST_Buffer

Introduction: Returns a geometry/geography that represents all points whose distance from this Geometry/geography is less than or equal to distance. The function supports both Planar/Euclidean and Spheroidal/Geodesic buffering (Since v1.6.0). Spheroidal buffer also supports geometries crossing the International Date Line (IDL).

Mode of buffer calculation (Since: v1.6.0):

The optional third parameter, useSpheroid, controls the mode of buffer calculation.

• Planar Buffering (default): When useSpheroid is false, ST_Buffer performs standard planar buffering based on the provided parameters.
• Spheroidal Buffering:
  • When useSpheroid is set to true, the function returns the spheroidal buffer polygon for more accurate representation over the Earth. In this mode, the unit of the buffer distance is interpreted as meters.
  • ST_Buffer first determines the most appropriate Spatial Reference Identifier (SRID) for a given geometry, based on its spatial extent and location, using ST_BestSRID.
  • The geometry is then transformed from its original SRID to the selected SRID. If the input geometry does not have a set SRID, ST_Buffer defaults to using WGS 84 (SRID 4326) as its original SRID.
  • The standard planar buffer operation is then applied in this coordinate system.
  • Finally, the buffered geometry is transformed back to its original SRID, or to WGS 84 if the original SRID was not set.

Note

Spheroidal buffering only supports lon/lat coordinate systems and will throw an IllegalArgumentException for input geometries in meter based coordinate systems.

Note

Spheroidal buffering may not produce accurate output buffer for input geometries larger than a UTM zone.

Buffer Style Parameters:

The optional forth parameter controls the buffer accuracy and style. Buffer accuracy is specified by the number of line segments approximating a quarter circle, with a default of 8 segments. Buffer style can be set by providing blank-separated key=value pairs in a list format.

• quad_segs=# : Number of line segments utilized to approximate a quarter circle (default is 8).
• endcap=round|flat|square : End cap style (default is round). butt is an accepted synonym for flat.
• join=round|mitre|bevel : Join style (default is round). miter is an accepted synonym for mitre.
• mitre_limit=#.# : mitre ratio limit and it only affects mitred join style. miter_limit is an accepted synonym for mitre_limit.
• side=both|left|right : The option left or right enables a single-sided buffer operation on the geometry, with the buffered side aligned according to the direction of the line. This functionality is specific to LINESTRING geometry and has no impact on POINT or POLYGON geometries. By default, square end caps are applied.

Note

ST_Buffer throws an IllegalArgumentException if the correct format, parameters, or options are not provided.

Format:

ST_Buffer (A: Geometry, buffer: Double)

ST_Buffer (A: Geometry, buffer: Double, useSpheroid: Boolean)

ST_Buffer (A: Geometry, buffer: Double, useSpheroid: Boolean, bufferStyleParameters: String)

Since: v1.5.1

SQL Example:

SELECT ST_Buffer(ST_GeomFromWKT('POINT(0 0)'), 10)
SELECT ST_Buffer(ST_GeomFromWKT('POINT(0 0)'), 10, false, 'quad_segs=2')

Output:

8 Segments   2 Segments

SQL Example:

SELECT ST_Buffer(ST_GeomFromWKT('LINESTRING(0 0, 50 70, 100 100)'), 10, false, 'side=left')

Output:

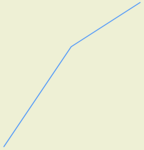
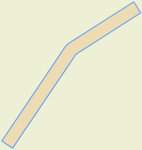
Original Linestring   Left side buffed Linestring

ST_BuildArea

Introduction: Returns the areal geometry formed by the constituent linework of the input geometry.

Format: ST_BuildArea (A:geometry)

Example:

SELECT ST_BuildArea(
    ST_GeomFromText('MULTILINESTRING((0 0, 20 0, 20 20, 0 20, 0 0),(2 2, 18 2, 18 18, 2 18, 2 2))')
) AS geom

Result:

+----------------------------------------------------------------------------+
|geom                                                                        |
+----------------------------------------------------------------------------+
|POLYGON((0 0,0 20,20 20,20 0,0 0),(2 2,18 2,18 18,2 18,2 2))                |
+----------------------------------------------------------------------------+

ST_Centroid

Introduction: Return the centroid point of A

Format: ST_Centroid (A:geometry)

SQL example:

SELECT ST_Centroid(polygondf.countyshape)
FROM polygondf

ST_ClosestPoint

Introduction: Returns the 2-dimensional point on geom1 that is closest to geom2. This is the first point of the shortest line between the geometries. If using 3D geometries, the Z coordinates will be ignored. If you have a 3D Geometry, you may prefer to use ST_3DClosestPoint. It will throw an exception indicates illegal argument if one of the params is an empty geometry.

Format: ST_ClosestPoint(g1: Geometry, g2: Geometry)

SQL Example:

SELECT ST_AsText( ST_ClosestPoint(g1, g2)) As ptwkt;

Input: g1: POINT (160 40), g2: LINESTRING (10 30, 50 50, 30 110, 70 90, 180 140, 130 190)

Output: POINT(160 40)

Input: g1: LINESTRING (10 30, 50 50, 30 110, 70 90, 180 140, 130 190), g2: POINT (160 40)

Output: POINT(125.75342465753425 115.34246575342466)

Input: g1: 'POLYGON ((190 150, 20 10, 160 70, 190 150))', g2: ST_Buffer('POINT(80 160)', 30)

Output: POINT(131.59149149528952 101.89887534906197)

ST_Collect

Introduction:

Build an appropriate Geometry, MultiGeometry, or GeometryCollection to contain the Geometrys in it. For example:

• If geomList contains a single Polygon, the Polygon is returned.
• If geomList contains several Polygons, a MultiPolygon is returned.
• If geomList contains some Polygons and some LineStrings, a GeometryCollection is returned.
• If geomList is empty, an empty GeometryCollection is returned.

Note that this method does not "flatten" Geometries in the input, and hence if any MultiGeometries are contained in the input, a GeometryCollection containing them will be returned.

Format

ST_Collect(*geom: geometry)

Example:

WITH src_tbl AS (
    SELECT sedona.ST_GeomFromText('POINT (40 10)') AS geom
    UNION
    SELECT sedona.ST_GeomFromText('LINESTRING (0 5, 0 10)') AS geom
)
SELECT sedona.ST_AsText(collection)
FROM src_tbl,
     TABLE(sedona.ST_Collect(src_tbl.geom) OVER (PARTITION BY 1));

Result:

GEOMETRYCOLLECTION (POINT (40 10), LINESTRING (0 5, 0 10))

ST_CollectionExtract

Introduction: Returns a homogeneous multi-geometry from a given geometry collection.

The type numbers are:

1. POINT
2. LINESTRING
3. POLYGON

If the type parameter is omitted a multi-geometry of the highest dimension is returned.

Format: ST_CollectionExtract (A:geometry)

Format: ST_CollectionExtract (A:geometry, type:Int)

Example:

WITH test_data as (
    ST_GeomFromText(
        'GEOMETRYCOLLECTION(POINT(40 10), POLYGON((0 0, 0 5, 5 5, 5 0, 0 0)))'
    ) as geom
)
SELECT ST_CollectionExtract(geom) as c1, ST_CollectionExtract(geom, 1) as c2
FROM test_data

Result:

+----------------------------------------------------------------------------+
|c1                                        |c2                               |
+----------------------------------------------------------------------------+
|MULTIPOLYGON(((0 0, 0 5, 5 5, 5 0, 0 0))) |MULTIPOINT(40 10)                |              |
+----------------------------------------------------------------------------+

ST_ConcaveHull

Introduction: Return the Concave Hull of polygon A, with alpha set to pctConvex[0, 1] in the Delaunay Triangulation method, the concave hull will not contain a hole unless allowHoles is set to true

Format: ST_ConcaveHull (A:geometry, pctConvex:float)

Format: ST_ConcaveHull (A:geometry, pctConvex:float, allowHoles:Boolean)

SQL example:

SELECT ST_ConcaveHull(polygondf.countyshape, pctConvex)`
FROM polygondf

ST_ConvexHull

Introduction: Return the Convex Hull of polygon A

Format: ST_ConvexHull (A:geometry)

SQL example:

SELECT ST_ConvexHull(polygondf.countyshape)
FROM polygondf

ST_CoordDim

Introduction: Returns the coordinate dimensions of the geometry. It is an alias of ST_NDims.

Format: ST_CoordDim(geom: Geometry)

SQL Example with x, y, z coordinate:

SELECT ST_CoordDim(ST_GeomFromText('POINT(1 1 2'))

Output:

3

SQL Example with x, y coordinate:

SELECT ST_CoordDim(ST_GeomFromWKT('POINT(3 7)'))

Output:

2

ST_CrossesDateLine

Introduction: This function determines if a given geometry crosses the International Date Line. It operates by checking if the difference in longitude between any pair of consecutive points in the geometry exceeds 180 degrees. If such a difference is found, it is assumed that the geometry crosses the Date Line. It returns true if the geometry crosses the Date Line, and false otherwise.

Note

The function assumes that the provided geometry is in lon/lat coordinate reference system where longitude values range from -180 to 180 degrees.

Note

For multi-geometries (e.g., MultiPolygon, MultiLineString), this function will return true if any one of the geometries within the multi-geometry crosses the International Date Line.

Format: ST_CrossesDateLine(geometry: Geometry)

Since: v1.6.0

SQL Example:

SELECT ST_CrossesDateLine(ST_GeomFromWKT('LINESTRING(170 30, -170 30)'))

Output:

true

Warning

For geometries that span more than 180 degrees in longitude without actually crossing the Date Line, this function may still return true, indicating a crossing.

ST_Degrees

Introduction: Convert an angle in radian to degrees.

Format: ST_Degrees(angleInRadian)

SQL Example:

SELECT ST_Degrees(0.19739555984988044)

Output:

11.309932474020195

ST_DelaunayTriangles

Introduction: This function computes the Delaunay triangulation for the set of vertices in the input geometry. An optional tolerance parameter allows snapping nearby input vertices together prior to triangulation and can improve robustness in certain scenarios by handling near-coincident vertices. The default for tolerance is 0. The Delaunay triangulation geometry is bounded by the convex hull of the input vertex set.

The output geometry representation depends on the provided flag:

• 0 - a GeometryCollection of triangular Polygons (default option)
• 1 - a MultiLinestring of the edges of the triangulation

Format:

ST_DelaunayTriangles(geometry: Geometry)

ST_DelaunayTriangles(geometry: Geometry, tolerance: Double)

ST_DelaunayTriangles(geometry: Geometry, tolerance: Double, flag: Integer)

SQL Example

SELECT ST_DelaunayTriangles(
        ST_GeomFromWKT('POLYGON ((10 10, 15 30, 20 25, 25 35, 30 20, 40 30, 50 10, 45 5, 35 15, 30 5, 25 15, 20 10, 15 20, 10 10))')
)

Output:

GEOMETRYCOLLECTION (POLYGON ((15 30, 10 10, 15 20, 15 30)), POLYGON ((15 30, 15 20, 20 25, 15 30)), POLYGON ((15 30, 20 25, 25 35, 15 30)), POLYGON ((25 35, 20 25, 30 20, 25 35)), POLYGON ((25 35, 30 20, 40 30, 25 35)), POLYGON ((40 30, 30 20, 35 15, 40 30)), POLYGON ((40 30, 35 15, 50 10, 40 30)), POLYGON ((50 10, 35 15, 45 5, 50 10)), POLYGON ((30 5, 45 5, 35 15, 30 5)), POLYGON ((30 5, 35 15, 25 15, 30 5)), POLYGON ((30 5, 25 15, 20 10, 30 5)), POLYGON ((30 5, 20 10, 10 10, 30 5)), POLYGON ((10 10, 20 10, 15 20, 10 10)), POLYGON ((15 20, 20 10, 25 15, 15 20)), POLYGON ((15 20, 25 15, 20 25, 15 20)), POLYGON ((20 25, 25 15, 30 20, 20 25)), POLYGON ((30 20, 25 15, 35 15, 30 20)))

ST_Difference

Introduction: Return the difference between geometry A and B (return part of geometry A that does not intersect geometry B)

Format: ST_Difference (A:geometry, B:geometry)

Example:

SELECT ST_Difference(ST_GeomFromWKT('POLYGON ((-3 -3, 3 -3, 3 3, -3 3, -3 -3))'), ST_GeomFromWKT('POLYGON ((0 -4, 4 -4, 4 4, 0 4, 0 -4))'))

Result:

POLYGON ((0 -3, -3 -3, -3 3, 0 3, 0 -3))

ST_Dimension

Introduction: Return the topological dimension of this Geometry object, which must be less than or equal to the coordinate dimension. OGC SPEC s2.1.1.1 - returns 0 for POINT, 1 for LINESTRING, 2 for POLYGON, and the largest dimension of the components of a GEOMETRYCOLLECTION. If the dimension is unknown (e.g. for an empty GEOMETRYCOLLECTION) 0 is returned.

Format: ST_Dimension (A: Geometry) | ST_Dimension (C: Geometrycollection)

SQL Example:

SELECT ST_Dimension('GEOMETRYCOLLECTION(LINESTRING(1 1,0 0),POINT(0 0))');

Output:

1

ST_Distance

Introduction: Return the Euclidean distance between A and B

Format: ST_Distance (A:geometry, B:geometry)

SQL example:

SELECT ST_Distance(polygondf.countyshape, polygondf.countyshape)
FROM polygondf

ST_DistanceSphere

Introduction: Return the haversine / great-circle distance of A using a given earth radius (default radius: 6371008.0). Unit is meter. Compared to ST_Distance + ST_Transform, it works better for datasets that cover large regions such as continents or the entire planet. It is equivalent to PostGIS ST_Distance(geography, use_spheroid=false) and ST_DistanceSphere function and produces nearly identical results. It provides faster but less accurate result compared to ST_DistanceSpheroid.

Geometry must be in EPSG:4326 (WGS84) projection and must be in lat/lon order. You can use ST_FlipCoordinates to swap lat and lon. For non-point data, we first take the centroids of both geometries and then compute the distance.

Format: ST_DistanceSphere (A:geometry)

SQL example 1:

SELECT ST_DistanceSphere(ST_GeomFromWKT('POINT (51.3168 -0.56)'), ST_GeomFromWKT('POINT (55.9533 -3.1883)'))

Output: 543796.9506134904

SQL example 2:

SELECT ST_DistanceSphere(ST_GeomFromWKT('POINT (51.3168 -0.56)'), ST_GeomFromWKT('POINT (55.9533 -3.1883)'), 6378137.0)

Output: 544405.4459192449

ST_DistanceSpheroid

Introduction: Return the geodesic distance of A using WGS84 spheroid. Unit is meter. Compared to ST_Distance + ST_Transform, it works better for datasets that cover large regions such as continents or the entire planet. It is equivalent to PostGIS ST_Distance(geography, use_spheroid=true) and ST_DistanceSpheroid function and produces nearly identical results. It provides slower but more accurate result compared to ST_DistanceSphere.

Geometry must be in EPSG:4326 (WGS84) projection and must be in lat/lon order. You can use ST_FlipCoordinates to swap lat and lon. For non-point data, we first take the centroids of both geometries and then compute the distance.

Format: ST_DistanceSpheroid (A:geometry)

SQL example:

SELECT ST_DistanceSpheroid(ST_GeomFromWKT('POINT (51.3168 -0.56)'), ST_GeomFromWKT('POINT (55.9533 -3.1883)'))

Output: 544430.9411996207

ST_Dump

Introduction: This function takes a GeometryCollection/Multi Geometry object and returns a set of geometries containing the individual geometries that make up the input geometry. The function is useful for breaking down a GeometryCollection/Multi Geometry into its constituent geometries.

Format: ST_Dump(geom: geometry)

SQL example:

SELECT sedona.ST_AsText(geom)
FROM table(sedona.ST_Dump(sedona.ST_GeomFromText('MULTIPOINT ((10 40), (40 30), (20 20), (30 10))')));

Output:

POINT (10 40)
POINT (40 30)
POINT (20 20)
POINT (30 10)

ST_DumpPoints

Introduction: Returns a MultiPoint geometry which consists of individual points that compose the input line string.

Format: ST_DumpPoints(geom: geometry)

SQL example:

SELECT ST_DumpPoints(ST_GeomFromText('LINESTRING (0 0, 1 1, 1 0)'))

Output: MultiPoint ((0 0), (0 1), (1 1), (1 0), (0 0))

ST_EndPoint

Introduction: Returns last point of given linestring.

Format: ST_EndPoint(geom: geometry)

SQL example:

SELECT ST_EndPoint(ST_GeomFromText('LINESTRING(100 150,50 60, 70 80, 160 170)'))

Output: POINT(160 170)

ST_Envelope

Introduction: Return the envelope boundary of A

Format: ST_Envelope (A:geometry)

SQL example:

SELECT ST_Envelope(polygondf.countyshape)
FROM polygondf

ST_Expand

Introduction: Returns a geometry expanded from the bounding box of the input. The expansion can be specified in two ways:

1. By individual axis using deltaX, deltaY, or deltaZ parameters.
2. Uniformly across all axes using the uniformDelta parameter.

Format:

ST_Expand(geometry: Geometry, uniformDelta: Double)

ST_Expand(geometry: Geometry, deltaX: Double, deltaY: Double)

ST_Expand(geometry: Geometry, deltaX: Double, deltaY: Double, deltaZ: Double)

Note

Things to consider when using this function:

1. The uniformDelta parameter expands Z dimensions for XYZ geometries; otherwise, it only affects XY dimensions.
2. For XYZ geometries, specifying only deltaX and deltaY will preserve the original Z dimension.
3. If the input geometry has an M dimension then using this function will drop the said M dimension.

SQL Example:

SELECT ST_Expand(
        ST_GeomFromWKT('POLYGON Z((50 50 1, 50 80 2, 80 80 3, 80 50 2, 50 50 1))'),
        10
   )

Output:

POLYGON Z((40 40 -9, 40 90 -9, 90 90 13, 90 40 13, 40 40 -9))

ST_ExteriorRing

Introduction: Returns a line string representing the exterior ring of the POLYGON geometry. Return NULL if the geometry is not a polygon.

Format: ST_ExteriorRing(geom: geometry)

SQL example:

SELECT ST_ExteriorRing(ST_GeomFromText('POLYGON((0 0 1, 1 1 1, 1 2 1, 1 1 1, 0 0 1))'))

Output: LINESTRING (0 0, 1 1, 1 2, 1 1, 0 0)

ST_FlipCoordinates

Introduction: Returns a version of the given geometry with X and Y axis flipped.

Format: ST_FlipCoordinates(A:geometry)

SQL example:

SELECT ST_FlipCoordinates(df.geometry)
FROM df

Input: POINT (1 2)

Output: POINT (2 1)

ST_Force_2D

Introduction: Forces the geometries into a "2-dimensional mode" so that all output representations will only have the X and Y coordinates

Format: ST_Force_2D (A:geometry)

Example:

SELECT ST_AsText(
    ST_Force_2D(ST_GeomFromText('POLYGON((0 0 2,0 5 2,5 0 2,0 0 2),(1 1 2,3 1 2,1 3 2,1 1 2))'))
) AS geom

Result:

+---------------------------------------------------------------+
|geom                                                           |
+---------------------------------------------------------------+
|POLYGON((0 0,0 5,5 0,0 0),(1 1,3 1,1 3,1 1))                   |
+---------------------------------------------------------------+

ST_Force3D

Introduction: Forces the geometry into a 3-dimensional model so that all output representations will have X, Y and Z coordinates. An optionally given zValue is tacked onto the geometry if the geometry is 2-dimensional. Default value of zValue is 0.0 If the given geometry is 3-dimensional, no change is performed on it. If the given geometry is empty, no change is performed on it.

Note

Example output is after calling ST_AsText() on returned geometry, which adds Z for in the WKT for 3D geometries

Format: ST_Force3D(geometry, zValue)

SQL Example:

SELECT ST_Force3D(geometry) AS geom

Input: LINESTRING(0 1, 1 2, 2 1)

Output: LINESTRING Z(0 1 0, 1 2 0, 2 1 0)

Input: POLYGON((0 0 2,0 5 2,5 0 2,0 0 2),(1 1 2,3 1 2,1 3 2,1 1 2))

Output: POLYGON Z((0 0 2,0 5 2,5 0 2,0 0 2),(1 1 2,3 1 2,1 3 2,1 1 2))

SELECT ST_Force3D(geometry, 2.3) AS geom

Input: LINESTRING(0 1, 1 2, 2 1)

Output: LINESTRING Z(0 1 2.3, 1 2 2.3, 2 1 2.3)

Input: POLYGON((0 0 2,0 5 2,5 0 2,0 0 2),(1 1 2,3 1 2,1 3 2,1 1 2))

Output: POLYGON Z((0 0 2,0 5 2,5 0 2,0 0 2),(1 1 2,3 1 2,1 3 2,1 1 2))

Input: LINESTRING EMPTY

Output: LINESTRING EMPTY

ST_Force3DZ

Introduction: Forces the geometry into a 3-dimensional model so that all output representations will have X, Y and Z coordinates. An optionally given zValue is tacked onto the geometry if the geometry is 2-dimensional. Default value of zValue is 0.0 If the given geometry is 3-dimensional, no change is performed on it. If the given geometry is empty, no change is performed on it. This function is an alias for ST_Force3D.

Note

Example output is after calling ST_AsText() on returned geometry, which adds Z for in the WKT for 3D geometries

Format: ST_Force3DZ(geometry: Geometry, zValue: Double)

SQL Example

SELECT ST_AsText(ST_Force3DZ(ST_GeomFromText('POLYGON((0 0 2,0 5 2,5 0 2,0 0 2),(1 1 2,3 1 2,1 3 2,1 1 2))'), 2.3))

Output:

POLYGON Z((0 0 2, 0 5 2, 5 0 2, 0 0 2), (1 1 2, 3 1 2, 1 3 2, 1 1 2))

SQL Example

SELECT ST_AsText(ST_Force3DZ(ST_GeomFromText('LINESTRING(0 1,1 0,2 0)'), 2.3))

Output:

LINESTRING Z(0 1 2.3, 1 0 2.3, 2 0 2.3)

ST_ForceCollection

Introduction: This function converts the input geometry into a GeometryCollection, regardless of the original geometry type. If the input is a multipart geometry, such as a MultiPolygon or MultiLineString, it will be decomposed into a GeometryCollection containing each individual Polygon or LineString element from the original multipart geometry.

Format: ST_ForceCollection(geom: Geometry)

SQL Example

SELECT ST_ForceCollection(
            ST_GeomFromWKT(
                "MULTIPOINT (30 10, 40 40, 20 20, 10 30, 10 10, 20 50)"
    )
)

Output:

GEOMETRYCOLLECTION (POINT (30 10), POINT (40 40), POINT (20 20), POINT (10 30), POINT (10 10), POINT (20 50))

ST_ForcePolygonCCW

Introduction: For (Multi)Polygon geometries, this function sets the exterior ring orientation to counter-clockwise and interior rings to clockwise orientation. Non-polygonal geometries are returned unchanged.

Format: ST_ForcePolygonCCW(geom: Geometry)

SQL Example:

SELECT ST_AsText(ST_ForcePolygonCCW(ST_GeomFromText('POLYGON ((20 35, 45 20, 30 5, 10 10, 10 30, 20 35), (30 20, 20 25, 20 15, 30 20))')))

Output:

POLYGON ((20 35, 10 30, 10 10, 30 5, 45 20, 20 35), (30 20, 20 15, 20 25, 30 20))

ST_ForcePolygonCW

Introduction: For (Multi)Polygon geometries, this function sets the exterior ring orientation to clockwise and interior rings to counter-clockwise orientation. Non-polygonal geometries are returned unchanged.

Format: ST_ForcePolygonCW(geom: Geometry)

SQL Example:

SELECT ST_AsText(ST_ForcePolygonCW(ST_GeomFromText('POLYGON ((20 35, 10 30, 10 10, 30 5, 45 20, 20 35),(30 20, 20 15, 20 25, 30 20))')))

Output:

POLYGON ((20 35, 45 20, 30 5, 10 10, 10 30, 20 35), (30 20, 20 25, 20 15, 30 20))

ST_ForceRHR

Introduction: Sets the orientation of polygon vertex orderings to follow the Right-Hand-Rule convention. The exterior ring will have a clockwise winding order, while any interior rings are oriented counter-clockwise. This ensures the area bounded by the polygon falls on the right-hand side relative to the ring directions. The function is an alias for ST_ForcePolygonCW.

Format: ST_ForceRHR(geom: Geometry)

SQL Example:

SELECT ST_AsText(ST_ForceRHR(ST_GeomFromText('POLYGON ((20 35, 10 30, 10 10, 30 5, 45 20, 20 35),(30 20, 20 15, 20 25, 30 20))')))

Output:

POLYGON ((20 35, 45 20, 30 5, 10 10, 10 30, 20 35), (30 20, 20 25, 20 15, 30 20))

ST_FrechetDistance

Introduction: Computes and returns discrete Frechet Distance between the given two geometries, based on Computing Discrete Frechet Distance

If any of the geometries is empty, returns 0.0

Format: ST_FrechetDistance(g1: Geometry, g2: Geometry)

SQL Example:

SELECT ST_FrechetDistance(ST_GeomFromWKT('POINT (0 1)'), ST_GeomFromWKT('LINESTRING (0 0, 1 0, 2 0, 3 0, 4 0, 5 0)'))

Output:

5.0990195135927845

ST_GeneratePoints

Introduction: Generates a specified quantity of pseudo-random points within the boundaries of the provided polygonal geometry. When seed is either zero or not defined then output will be random.

Format:

ST_GeneratePoints(geom: Geometry, numPoints: Integer, seed: Long = 0)

ST_GeneratePoints(geom: Geometry, numPoints: Integer)

SQL Example:

SELECT ST_GeneratePoints(
        ST_GeomFromWKT('POLYGON((0 0, 1 0, 1 1, 0 1, 0 0))'), 4
)

Output:

Note

Due to the pseudo-random nature of point generation, the output of this function will vary between executions and may not match any provided examples.

MULTIPOINT ((0.2393028905520183 0.9721563442837837), (0.3805848547053376 0.7546556656982678), (0.0950295778200995 0.2494334895495989), (0.4133520939987385 0.3447046312451945))

ST_GeoHash

Introduction: Returns GeoHash of the geometry with given precision

Format: ST_GeoHash(geom: geometry, precision: int)

Example:

Query:

SELECT ST_GeoHash(ST_GeomFromText('POINT(21.427834 52.042576573)'), 5) AS geohash

Result:

+-----------------------------+
|geohash                      |
+-----------------------------+
|u3r0p                        |
+-----------------------------+

ST_GeometricMedian

Introduction: Computes the approximate geometric median of a MultiPoint geometry using the Weiszfeld algorithm. The geometric median provides a centrality measure that is less sensitive to outlier points than the centroid.

The algorithm will iterate until the distance change between successive iterations is less than the supplied tolerance parameter. If this condition has not been met after maxIter iterations, the function will produce an error and exit, unless failIfNotConverged is set to false.

If a tolerance value is not provided, a default tolerance value is 1e-6.

Format: ST_GeometricMedian(geom: geometry, tolerance: float, maxIter: integer, failIfNotConverged: boolean)

Format: ST_GeometricMedian(geom: geometry, tolerance: float, maxIter: integer)

Format: ST_GeometricMedian(geom: geometry, tolerance: float)

Format: ST_GeometricMedian(geom: geometry)

Default parameters: tolerance: 1e-6, maxIter: 1000, failIfNotConverged: false

Example:

SELECT ST_GeometricMedian(ST_GeomFromWKT('MULTIPOINT((0 0), (1 1), (2 2), (200 200))'))

Output:

POINT (1.9761550281255005 1.9761550281255005)

ST_GeometryN

Introduction: Return the 0-based Nth geometry if the geometry is a GEOMETRYCOLLECTION, (MULTI)POINT, (MULTI)LINESTRING, MULTICURVE or (MULTI)POLYGON. Otherwise, return null

Format: ST_GeometryN(geom: geometry, n: Int)

SQL example:

SELECT ST_GeometryN(ST_GeomFromText('MULTIPOINT((1 2), (3 4), (5 6), (8 9))'), 1)

Output: POINT (3 4)

ST_GeometryType

Introduction: Returns the type of the geometry as a string. EG: 'ST_Linestring', 'ST_Polygon' etc.

Format: ST_GeometryType (A:geometry)

SQL example:

SELECT ST_GeometryType(polygondf.countyshape)
FROM polygondf

ST_HasZ

Introduction: Checks for the presence of Z coordinate values representing measures or linear references. Returns true if the input geometry includes an Z coordinate, false otherwise.

Format: ST_HasZ(geom: Geometry)

SQL Example

SELECT ST_HasZ(
        ST_GeomFromWKT('LINESTRING Z (30 10 5, 40 40 10, 20 40 15, 10 20 20)')
)

Output:

True

ST_HausdorffDistance

Introduction: Returns a discretized (and hence approximate) Hausdorff distance between the given 2 geometries. Optionally, a densityFraction parameter can be specified, which gives more accurate results by densifying segments before computing hausdorff distance between them. Each segment is broken down into equal-length subsegments whose ratio with segment length is closest to the given density fraction.

Hence, the lower the densityFrac value, the more accurate is the computed hausdorff distance, and the more time it takes to compute it.

If any of the geometry is empty, 0.0 is returned.

Note

Accepted range of densityFrac is (0.0, 1.0], if any other value is provided, ST_HausdorffDistance throws an IllegalArgumentException

Note

Even though the function accepts 3D geometry, the z ordinate is ignored and the computed hausdorff distance is equivalent to the geometries not having the z ordinate.

Format: ST_HausdorffDistance(g1: Geometry, g2: Geometry, densityFrac: Double)

SQL Example:

SELECT ST_HausdorffDistance(ST_GeomFromWKT('POINT (0.0 1.0)'), ST_GeomFromWKT('LINESTRING (0 0, 1 0, 2 0, 3 0, 4 0, 5 0)'), 0.1)

Output:

5.0990195135927845

SQL Example:

SELECT ST_HausdorffDistance(ST_GeomFromText('POLYGON Z((1 0 1, 1 1 2, 2 1 5, 2 0 1, 1 0 1))'), ST_GeomFromText('POLYGON Z((4 0 4, 6 1 4, 6 4 9, 6 1 3, 4 0 4))'))

Output:

5.0

ST_InteriorRingN

Introduction: Returns the Nth interior linestring ring of the polygon geometry. Returns NULL if the geometry is not a polygon or the given N is out of range

Format: ST_InteriorRingN(geom: geometry, n: Int)

SQL example:

SELECT ST_InteriorRingN(ST_GeomFromText('POLYGON((0 0, 0 5, 5 5, 5 0, 0 0), (1 1, 2 1, 2 2, 1 2, 1 1), (1 3, 2 3, 2 4, 1 4, 1 3), (3 3, 4 3, 4 4, 3 4, 3 3))'), 0)

Output: LINESTRING (1 1, 2 1, 2 2, 1 2, 1 1)

ST_Intersection

Introduction: Return the intersection geometry of A and B

Format: ST_Intersection (A:geometry, B:geometry)

SQL example:

SELECT ST_Intersection(polygondf.countyshape, polygondf.countyshape)
FROM polygondf

ST_IsClosed

Introduction: RETURNS true if the LINESTRING start and end point are the same.

Format: ST_IsClosed(geom: geometry)

SQL example:

SELECT ST_IsClosed(ST_GeomFromText('LINESTRING(0 0, 1 1, 1 0)'))

Output: false

ST_IsCollection

Introduction: Returns TRUE if the geometry type of the input is a geometry collection type. Collection types are the following:

• GEOMETRYCOLLECTION
• MULTI{POINT, POLYGON, LINESTRING}

Format: ST_IsCollection(geom: Geometry)

SQL Example:

SELECT ST_IsCollection(ST_GeomFromText('MULTIPOINT(0 0), (6 6)'))

Output:

true

SQL Example:

SELECT ST_IsCollection(ST_GeomFromText('POINT(5 5)'))

Output:

false

ST_IsEmpty

Introduction: Test if a geometry is empty geometry

Format: ST_IsEmpty (A:geometry)

SQL example:

SELECT ST_IsEmpty(polygondf.countyshape)
FROM polygondf

ST_IsPolygonCCW

Introduction: Returns true if all polygonal components in the input geometry have their exterior rings oriented counter-clockwise and interior rings oriented clockwise.

Format: ST_IsPolygonCCW(geom: Geometry)

SQL Example:

SELECT ST_IsPolygonCCW(ST_GeomFromWKT('POLYGON ((20 35, 10 30, 10 10, 30 5, 45 20, 20 35), (30 20, 20 15, 20 25, 30 20))'))

Output:

true

ST_IsPolygonCW

Introduction: Returns true if all polygonal components in the input geometry have their exterior rings oriented counter-clockwise and interior rings oriented clockwise.

Format: ST_IsPolygonCW(geom: Geometry)

SQL Example:

SELECT ST_IsPolygonCW(ST_GeomFromWKT('POLYGON ((20 35, 45 20, 30 5, 10 10, 10 30, 20 35), (30 20, 20 25, 20 15, 30 20))'))

Output:

true

ST_IsRing

Introduction: RETURN true if LINESTRING is ST_IsClosed and ST_IsSimple.

Format: ST_IsRing(geom: geometry)

SQL example:

SELECT ST_IsRing(ST_GeomFromText('LINESTRING(0 0, 0 1, 1 1, 1 0, 0 0)'))

Output: true

ST_IsSimple

Introduction: Test if geometry's only self-intersections are at boundary points.

Format: ST_IsSimple (A:geometry)

SQL example:

SELECT ST_IsSimple(polygondf.countyshape)
FROM polygondf

ST_IsValid

Introduction: Test if a geometry is well-formed. The function can be invoked with just the geometry or with an additional flag (from v1.5.1). The flag alters the validity checking behavior. The flags parameter is a bitfield with the following options:

• 0 (default): Use usual OGC SFS (Simple Features Specification) validity semantics.
• 1: "ESRI flag", Accepts certain self-touching rings as valid, which are considered invalid under OGC standards.

Formats:

ST_IsValid (A: Geometry)

ST_IsValid (A: Geometry, flag: Integer)

SQL Example:

SELECT ST_IsValid(ST_GeomFromWKT('POLYGON((0 0, 10 0, 10 10, 0 10, 0 0), (15 15, 15 20, 20 20, 20 15, 15 15))'))

Output:

false

ST_IsValidDetail

Introduction: Returns a row, containing a boolean valid stating if a geometry is valid, a string reason stating why it is invalid and a geometry location pointing out where it is invalid.

This function is a combination of ST_IsValid and ST_IsValidReason.

The flags parameter is a bitfield with the following options:

• 0: Use usual OGC SFS (Simple Features Specification) validity semantics.
• 1: "ESRI flag", Accepts certain self-touching rings as valid, which are considered invalid under OGC standards.

Format:

SELECT valid, reason, Sedonm.ST_AsText(location) AS location
FROM table(Sedona.ST_IsValidDetail(geom: Geometry, flag: Integer))

SQL Example:

SELECT valid, reason, Sedonm.ST_AsText(location) AS location
     FROM table(Sedona.ST_IsValidDetail(Sedona.ST_GeomFromWKT('POLYGON ((30 10, 40 40, 20 40, 30 10, 10 20, 30 10))'), 0))

Output:

+-----+---------------------------------------------------------+-------------+
|valid|reason                                                   |location     |
+-----+---------------------------------------------------------+-------------+
|false|Ring Self-intersection at or near point (30.0, 10.0, NaN)|POINT (30 10)|
+-----+---------------------------------------------------------+-------------+

ST_IsValidReason

Introduction: Returns text stating if the geometry is valid. If not, it provides a reason why it is invalid. The function can be invoked with just the geometry or with an additional flag. The flag alters the validity checking behavior. The flags parameter is a bitfield with the following options:

• 0 (default): Use usual OGC SFS (Simple Features Specification) validity semantics.
• 1: "ESRI flag", Accepts certain self-touching rings as valid, which are considered invalid under OGC standards.

Formats:

ST_IsValidReason (A: Geometry)

ST_IsValidReason (A: Geometry, flag: Integer)

SQL Example for valid geometry:

SELECT ST_IsValidReason(ST_GeomFromWKT('POLYGON ((100 100, 100 300, 300 300, 300 100, 100 100))')) as validity_info

Output:

Valid Geometry

SQL Example for invalid geometries:

SELECT gid, ST_IsValidReason(geom) as validity_info
FROM Geometry_table
WHERE ST_IsValid(geom) = false
ORDER BY gid

Output:

gid  |                  validity_info
-----+----------------------------------------------------
5330 | Self-intersection at or near point (32.0, 5.0, NaN)
5340 | Self-intersection at or near point (42.0, 5.0, NaN)
5350 | Self-intersection at or near point (52.0, 5.0, NaN)

ST_Length

Introduction: Returns the perimeter of A.

Format: ST_Length (A:geometry)

SQL example:

SELECT ST_Length(polygondf.countyshape)
FROM polygondf

ST_Length2D

Introduction: Returns the perimeter of A. This function is an alias of ST_Length.

Format: ST_Length2D (A:geometry)

SQL example:

SELECT ST_Length2D(polygondf.countyshape)
FROM polygondf

ST_LengthSpheroid

Introduction: Return the geodesic perimeter of A using WGS84 spheroid. Unit is meter. Works better for large geometries (country level) compared to ST_Length + ST_Transform. It is equivalent to PostGIS ST_Length(geography, use_spheroid=true) and ST_LengthSpheroid function and produces nearly identical results.

Geometry must be in EPSG:4326 (WGS84) projection and must be in lat/lon order. You can use ST_FlipCoordinates to swap lat and lon.

Format: ST_LengthSpheroid (A:geometry)

SQL example:

SELECT ST_LengthSpheroid(ST_GeomFromWKT('Polygon ((0 0, 0 90, 0 0))'))

Output: 20037508.342789244

ST_LineFromMultiPoint

Introduction: Creates a LineString from a MultiPoint geometry.

Format: ST_LineFromMultiPoint (A:geometry)

Example:

SELECT ST_AsText(
    ST_LineFromMultiPoint(ST_GeomFromText('MULTIPOINT((10 40), (40 30), (20 20), (30 10))'))
) AS geom

Result:

+---------------------------------------------------------------+
|geom                                                           |
+---------------------------------------------------------------+
|LINESTRING (10 40, 40 30, 20 20, 30 10)                        |
+---------------------------------------------------------------+

ST_LineInterpolatePoint

Introduction: Returns a point interpolated along a line. First argument must be a LINESTRING. Second argument is a Double between 0 and 1 representing fraction of total linestring length the point has to be located.

Format: ST_LineInterpolatePoint (geom: geometry, fraction: Double)

SQL example:

SELECT ST_LineInterpolatePoint(ST_GeomFromWKT('LINESTRING(25 50, 100 125, 150 190)'), 0.2) as Interpolated

Output:

+-----------------------------------------+
|Interpolated                             |
+-----------------------------------------+
|POINT (51.5974135047432 76.5974135047432)|
+-----------------------------------------+

ST_LineLocatePoint

Introduction: Returns a double between 0 and 1, representing the location of the closest point on the LineString as a fraction of its total length. The first argument must be a LINESTRING, and the second argument is a POINT geometry.

Format: ST_LineLocatePoint(linestring: Geometry, point: Geometry)

SQL Example:

SELECT ST_LineLocatePoint(ST_GeomFromWKT('LINESTRING(0 0, 1 1, 2 2)'), ST_GeomFromWKT('POINT(0 2)'))

Output:

0.5

ST_LineMerge

Introduction: Returns a LineString formed by sewing together the constituent line work of a MULTILINESTRING.

Note

Only works for MULTILINESTRING. Using other geometry will return a GEOMETRYCOLLECTION EMPTY. If the MultiLineString can't be merged, the original MULTILINESTRING is returned.

Format: ST_LineMerge (A:geometry)

SELECT ST_LineMerge(geometry)
FROM df

ST_LineSubstring

Introduction: Return a linestring being a substring of the input one starting and ending at the given fractions of total 2d length. Second and third arguments are Double values between 0 and 1. This only works with LINESTRINGs.

Format: ST_LineSubstring (geom: geometry, startfraction: Double, endfraction: Double)

SQL example:

SELECT ST_LineSubstring(ST_GeomFromWKT('LINESTRING(25 50, 100 125, 150 190)'), 0.333, 0.666) as Substring

ST_LongestLine

Introduction: Returns the LineString geometry representing the maximum distance between any two points from the input geometries.

Format: ST_LongestLine(geom1: Geometry, geom2: Geometry)

SQL Example:

SELECT ST_LongestLine(
        ST_GeomFromText("POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10))"),
        ST_GeomFromText("POLYGON ((10 20, 30 30, 40 20, 30 10, 10 20))")
)

Output:

LINESTRING (40 40, 10 20)

Output:

+------------------------------------------------------------------------------------------------+
|Substring                                                                                       |
+------------------------------------------------------------------------------------------------+
|LINESTRING (69.28469348539744 94.28469348539744, 100 125, 111.70035626068274 140.21046313888758)|
+------------------------------------------------------------------------------------------------+

ST_MakeLine

Introduction: Creates a LineString containing the points of Point, MultiPoint, or LineString geometries. Other geometry types cause an error.

Format:

ST_MakeLine(geom1: Geometry, geom2: Geometry)

ST_MakeLine(geoms: Geometry) This Geometry must be a GeometryCollection of the geometry types listed above.

SQL Example:

SELECT ST_AsText( ST_MakeLine(ST_Point(1,2), ST_Point(3,4)) );

Output:

LINESTRING(1 2,3 4)

SQL Example:

SELECT ST_AsText( ST_MakeLine( 'LINESTRING(0 0, 1 1)', 'LINESTRING(2 2, 3 3)' ) );

Output:

 LINESTRING(0 0,1 1,2 2,3 3)

ST_MakePolygon

Introduction: Function to convert closed linestring to polygon including holes. The holes must be a MultiLinestring.

Format: ST_MakePolygon(geom: geometry, holes: <geometry>)

Example:

Query:

SELECT
    ST_MakePolygon(
        ST_GeomFromText('LINESTRING(7 -1, 7 6, 9 6, 9 1, 7 -1)'),
        ST_GeomFromText('MultiLINESTRING((6 2, 8 2, 8 1, 6 1, 6 2))')
    ) AS polygon

Result:

+----------------------------------------------------------------+
|polygon                                                         |
+----------------------------------------------------------------+
|POLYGON ((7 -1, 7 6, 9 6, 9 1, 7 -1), (6 2, 8 2, 8 1, 6 1, 6 2))|
+----------------------------------------------------------------+

ST_MakeValid

Introduction: Given an invalid geometry, create a valid representation of the geometry.

Collapsed geometries are either converted to empty (keepCollapsed=true) or a valid geometry of lower dimension (keepCollapsed=false). Default is keepCollapsed=false.

Format: ST_MakeValid (A:geometry)

Format: ST_MakeValid (A:geometry, keepCollapsed:Boolean)

SQL example:

WITH linestring AS (
    SELECT ST_GeomFromWKT('LINESTRING(1 1, 1 1)') AS geom
) SELECT ST_MakeValid(geom), ST_MakeValid(geom, true) FROM linestring

Result:

+------------------+------------------------+
|st_makevalid(geom)|st_makevalid(geom, true)|
+------------------+------------------------+
|  LINESTRING EMPTY|             POINT (1 1)|
+------------------+------------------------+

Note

In Sedona up to and including version 1.2 the behaviour of ST_MakeValid was different. Be sure to check you code when upgrading. The previous implementation only worked for (multi)polygons and had a different interpretation of the second, boolean, argument. It would also sometimes return multiple geometries for a single geometry input.

ST_MaximumInscribedCircle

Introduction: Finds the largest circle that is contained within a (multi)polygon, or which does not overlap any lines and points. Returns a row with fields:

• center - center point of the circle
• nearest - nearest point from the center of the circle
• radius - radius of the circle

For polygonal geometries, the function inscribes the circle within the boundary rings, treating internal rings as additional constraints. When processing linear and point inputs, the algorithm inscribes the circle within the convex hull of the input, utilizing the input lines and points as additional boundary constraints.

Format: ST_MaximumInscribedCircle(geometry: Geometry)

Since: v1.6.1

SQL Example:

SELECT Sedona.ST_AsText(center) AS center, Sedona.ST_AsText(nearest) AS nearest, radius  FROM table(
    SELECT ST_MaximumIncribedCircle(ST_GeomFromWKT('POLYGON ((62.11 19.68, 60.79 17.20, 61.30 15.96, 62.11 16.08, 65.93 16.95, 66.20 20.61, 63.08 21.43, 64.48 18.70, 62.11 19.68))'))
)

Output:

+---------------------------------------------+-------------------------------------------+------------------+
|center                                       |nearest                                    |radius            |
+---------------------------------------------+-------------------------------------------+------------------+
|POINT (62.794975585937514 17.774780273437496)|POINT (63.36773534817729 19.15992378007859)|1.4988916836219184|
+---------------------------------------------+-------------------------------------------+------------------+

ST_MaxDistance

Introduction: Calculates and returns the length value representing the maximum distance between any two points across the input geometries. This function is an alias for ST_LongestDistance.

Format: ST_MaxDistance(geom1: Geometry, geom2: Geometry)

SQL Example:

SELECT ST_MaxDistance(
        ST_GeomFromText("POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10))"),
        ST_GeomFromText("POLYGON ((10 20, 30 30, 40 20, 30 10, 10 20))")
)

Output:

36.05551275463989

ST_MinimumClearance

Introduction: The minimum clearance is a metric that quantifies a geometry's tolerance to changes in coordinate precision or vertex positions. It represents the maximum distance by which vertices can be adjusted without introducing invalidity to the geometry's structure. A larger minimum clearance value indicates greater robustness against such perturbations.

For a geometry with a minimum clearance of x, the following conditions hold:

• No two distinct vertices are separated by a distance less than x.
• No vertex lies within a distance x from any line segment it is not an endpoint of.

For geometries with no definable minimum clearance, such as single Point geometries or MultiPoint geometries where all points occupy the same location, the function returns Double.MAX_VALUE.

Format: ST_MinimumClearance(geometry: Geometry)

SQL Example

SELECT ST_MinimumClearance(
        ST_GeomFromWKT('POLYGON ((65 18, 62 16, 64.5 16, 62 14, 65 14, 65 18))')
)

Output:

0.5

ST_MinimumClearanceLine

Introduction: This function returns a two-point LineString geometry representing the minimum clearance distance of the input geometry. If the input geometry does not have a defined minimum clearance, such as for single Points or coincident MultiPoints, an empty LineString geometry is returned instead.

Format: ST_MinimumClearanceLine(geometry: Geometry)

SQL Example:

SELECT ST_MinimumClearanceLine(
        ST_GeomFromWKT('POLYGON ((65 18, 62 16, 64.5 16, 62 14, 65 14, 65 18))')
)

Output:

LINESTRING (64.5 16, 65 16)

ST_MinimumBoundingCircle

Introduction: Returns the smallest circle polygon that contains a geometry.

Format: ST_MinimumBoundingCircle(geom: geometry, [Optional] quadrantSegments:int)

SQL example:

SELECT ST_MinimumBoundingCircle(ST_GeomFromText('POLYGON((1 1,0 0, -1 1, 1 1))'))

ST_MinimumBoundingRadius

Introduction: Returns two columns containing the center point and radius of the smallest circle that contains a geometry.

Format: ST_MinimumBoundingRadius(geom: geometry)

SQL example:

SELECT sedona.ST_AsText(center), radius
FROM table(sedona.ST_MinimumBoundingRadius(sedona.ST_GeomFromText('POLYGON ((0 0, 0 1, 1 1, 1 0, 0 0))')))

Result:

POINT (0.5 0.5), 0.7071067811865476

ST_Multi

Introduction: Returns a MultiGeometry object based on the geometry input. ST_Multi is basically an alias for ST_Collect with one geometry.

Format

ST_Multi(geom: geometry)

Example:

SELECT ST_Multi(
    ST_GeomFromText('POINT(1 1)')
) AS geom

Result:

+---------------------------------------------------------------+
|geom                                                           |
+---------------------------------------------------------------+
|MULTIPOINT (1 1)                                               |
+---------------------------------------------------------------+

ST_NDims

Introduction: Returns the coordinate dimension of the geometry.

Format: ST_NDims(geom: geometry)

SQL example with z co-rodinate:

SELECT ST_NDims(ST_GeomFromEWKT('POINT(1 1 2)'))

Output: 3

SQL example with x,y coordinate:

SELECT ST_NDims(ST_GeomFromText('POINT(1 1)'))

Output: 2

ST_Normalize

Introduction: Returns the input geometry in its normalized form.

Format

ST_Normalize(geom: geometry)

Example:

SELECT ST_AsEWKT(ST_Normalize(ST_GeomFromWKT('POLYGON((0 1, 1 1, 1 0, 0 0, 0 1))'))) AS geom

Result:

+-----------------------------------+
|geom                               |
+-----------------------------------+
|POLYGON ((0 0, 0 1, 1 1, 1 0, 0 0))|
+-----------------------------------+

ST_NPoints

Introduction: Return points of the geometry

Format: ST_NPoints (A:geometry)

SELECT ST_NPoints(polygondf.countyshape)
FROM polygondf

ST_NRings

Introduction: Returns the number of rings in a Polygon or MultiPolygon. Contrary to ST_NumInteriorRings, this function also takes into account the number of exterior rings.

This function returns 0 for an empty Polygon or MultiPolygon. If the geometry is not a Polygon or MultiPolygon, an IllegalArgument Exception is thrown.

Format: ST_NRings(geom: geometry)

Examples:

Input: POLYGON ((1 0, 1 1, 2 1, 2 0, 1 0))

Output: 1

Input: 'MULTIPOLYGON (((1 0, 1 6, 6 6, 6 0, 1 0), (2 1, 2 2, 3 2, 3 1, 2 1)), ((10 0, 10 6, 16 6, 16 0, 10 0), (12 1, 12 2, 13 2, 13 1, 12 1)))'

Output: 4

Input: 'POLYGON EMPTY'

Output: 0

Input: 'LINESTRING (1 0, 1 1, 2 1)'

Output: Unsupported geometry type: LineString, only Polygon or MultiPolygon geometries are supported.

ST_NumGeometries

Introduction: Returns the number of Geometries. If geometry is a GEOMETRYCOLLECTION (or MULTI*) return the number of geometries, for single geometries will return 1.

Format: ST_NumGeometries (A:geometry)

SELECT ST_NumGeometries(df.geometry)
FROM df

ST_NumInteriorRing

Introduction: Returns number of interior rings of polygon geometries. It is an alias of ST_NumInteriorRings.

Format: ST_NumInteriorRing(geom: Geometry)

SQL Example

SELECT ST_NumInteriorRing(ST_GeomFromText('POLYGON ((0 0, 0 5, 5 5, 5 0, 0 0), (1 1, 2 1, 2 2, 1 2, 1 1))'))

Output:

1

ST_NumInteriorRings

Introduction: RETURNS number of interior rings of polygon geometries.

Format: ST_NumInteriorRings(geom: geometry)

SQL example:

SELECT ST_NumInteriorRings(ST_GeomFromText('POLYGON ((0 0, 0 5, 5 5, 5 0, 0 0), (1 1, 2 1, 2 2, 1 2, 1 1))'))

Output: 1

ST_NumPoints

Introduction: Returns number of points in a LineString

Format: ST_NumPoints(geom: geometry)

Note

If any other geometry is provided as an argument, an IllegalArgumentException is thrown.

SQL Example:

SELECT ST_NumPoints(ST_GeomFromWKT('MULTIPOINT ((0 0), (1 1), (0 1), (2 2))'))

Output:

IllegalArgumentException: Unsupported geometry type: MultiPoint, only LineString geometry is supported.

SQL Example:

SELECT ST_NumPoints(ST_GeomFromText('LINESTRING(0 1, 1 0, 2 0)'))

Output: 3

ST_PointN

Introduction: Return the Nth point in a single linestring or circular linestring in the geometry. Negative values are counted backwards from the end of the LineString, so that -1 is the last point. Returns NULL if there is no linestring in the geometry.

Format: ST_PointN(geom: geometry, n: integer)

SQL example:

SELECT ST_PointN(ST_GeomFromText('LINESTRING(0 0, 1 2, 2 4, 3 6)'), 2) AS geom

Result:

+---------------------------------------------------------------+
|geom                                                           |
+---------------------------------------------------------------+
|POINT (1 2)                                                    |
+---------------------------------------------------------------+

ST_PointOnSurface

Introduction: Returns a POINT guaranteed to lie on the surface.

Format: ST_PointOnSurface(A:geometry)

Examples:

SELECT ST_AsText(ST_PointOnSurface(ST_GeomFromText('POINT(0 5)')));
 st_astext
------------
 POINT(0 5)

SELECT ST_AsText(ST_PointOnSurface(ST_GeomFromText('LINESTRING(0 5, 0 10)')));
 st_astext
------------
 POINT(0 5)

SELECT ST_AsText(ST_PointOnSurface(ST_GeomFromText('POLYGON((0 0, 0 5, 5 5, 5 0, 0 0))')));
   st_astext
----------------
 POINT(2.5 2.5)

SELECT ST_AsText(ST_PointOnSurface(ST_GeomFromText('LINESTRING(0 5 1, 0 0 1, 0 10 2)')));
   st_astext
----------------
 POINT Z(0 0 1)

ST_Points

Introduction: Returns a MultiPoint geometry consisting of all the coordinates of the input geometry. It preserves duplicate points as well as M and Z coordinates.

Format: ST_Points(geom: Geometry)

SQL Example

SELECT ST_AsText(ST_Points(ST_GeomFromEWKT('LINESTRING (2 4, 3 3, 4 2, 7 3)')));

Output:

MULTIPOINT ((2 4), (3 3), (4 2), (7,3))

ST_Polygon

Introduction: Function to create a polygon built from the given LineString and sets the spatial reference system from the srid

Format: ST_Polygon(geom: Geometry, srid: Integer)

SQL Example:

SELECT ST_AsText( ST_Polygon(ST_GeomFromEWKT('LINESTRING(75 29 1, 77 29 2, 77 29 3, 75 29 1)'), 4326) );

Output:

POLYGON((75 29 1, 77 29 2, 77 29 3, 75 29 1))

ST_Polygonize

Introduction: Generates a GeometryCollection composed of polygons that are formed from the linework of an input GeometryCollection. When the input does not contain any linework that forms a polygon, the function will return an empty GeometryCollection.

Note

ST_Polygonize function assumes that the input geometries form a valid and simple closed linestring that can be turned into a polygon. If the input geometries are not noded or do not form such linestrings, the resulting GeometryCollection may be empty or may not contain the expected polygons.

Format: ST_Polygonize(geom: Geometry)

Example:

SELECT ST_AsText(ST_Polygonize(ST_GeomFromEWKT('GEOMETRYCOLLECTION (LINESTRING (2 0, 2 1, 2 2), LINESTRING (2 2, 2 3, 2 4), LINESTRING (0 2, 1 2, 2 2), LINESTRING (2 2, 3 2, 4 2), LINESTRING (0 2, 1 3, 2 4), LINESTRING (2 4, 3 3, 4 2))')));

Output:

GEOMETRYCOLLECTION (POLYGON ((0 2, 1 3, 2 4, 2 3, 2 2, 1 2, 0 2)), POLYGON ((2 2, 2 3, 2 4, 3 3, 4 2, 3 2, 2 2)))

ST_ReducePrecision

Introduction: Reduce the decimals places in the coordinates of the geometry to the given number of decimal places. The last decimal place will be rounded. This function was called ST_PrecisionReduce in versions prior to v1.5.0.

Format: ST_ReducePrecision (A: Geometry, B: Integer)

SQL Example:

SELECT ST_ReducePrecision(ST_GeomFromWKT('Point(0.1234567890123456789 0.1234567890123456789)')
    , 9)

The new coordinates will only have 9 decimal places.

Output:

POINT (0.123456789 0.123456789)

ST_RemovePoint

Introduction: RETURN Line with removed point at given index, position can be omitted and then last one will be removed.

Format: ST_RemovePoint(geom: geometry, position: integer)

Format: ST_RemovePoint(geom: geometry)

SQL example:

SELECT ST_RemovePoint(ST_GeomFromText('LINESTRING(0 0, 1 1, 1 0)'), 1)

Output: LINESTRING(0 0, 1 0)

ST_Reverse

Introduction: Return the geometry with vertex order reversed

Format: ST_Reverse (A:geometry)

Example:

SELECT ST_AsText(
    ST_Reverse(ST_GeomFromText('LINESTRING(0 0, 1 2, 2 4, 3 6)'))
) AS geom

Result:

+---------------------------------------------------------------+
|geom                                                           |
+---------------------------------------------------------------+
|LINESTRING (3 6, 2 4, 1 2, 0 0)                                |
+---------------------------------------------------------------+

ST_Rotate

Introduction: Rotates a geometry by a specified angle in radians counter-clockwise around a given origin point. The origin for rotation can be specified as either a POINT geometry or x and y coordinates. If the origin is not specified, the geometry is rotated around POINT(0 0).

Formats;

ST_Rotate (geometry: Geometry, angle: Double)

ST_Rotate (geometry: Geometry, angle: Double, originX: Double, originY: Double)

ST_Rotate (geometry: Geometry, angle: Double, pointOrigin: Geometry)

SQL Example:

SELECT ST_Rotate(ST_GeomFromEWKT('SRID=4326;POLYGON ((0 0, 1 0, 1 1, 0 0))'), 10, 0, 0)

Output:

SRID=4326;POLYGON ((0 0, -0.8390715290764524 -0.5440211108893698, -0.2950504181870827 -1.383092639965822, 0 0))

ST_S2CellIDs

Introduction: Cover the geometry with Google S2 Cells, return the corresponding cell IDs with the given level. The level indicates the size of cells. With a bigger level, the cells will be smaller, the coverage will be more accurate, but the result size will be exponentially increasing.

Format: ST_S2CellIDs(geom: geometry, level: Int)

SQL example:

SELECT ST_S2CellIDs(ST_GeomFromText('LINESTRING(1 3 4, 5 6 7)'), 6)

Output:

+------------------------------------------------------------------------------------------------------------------------------+
|st_s2cellids(st_geomfromtext(LINESTRING(1 3 4, 5 6 7), 0), 6)                                                                 |
+------------------------------------------------------------------------------------------------------------------------------+
|[1159395429071192064, 1159958379024613376, 1160521328978034688, 1161084278931456000, 1170091478186196992, 1170654428139618304]|
+------------------------------------------------------------------------------------------------------------------------------+

ST_SetPoint

Introduction: Replace Nth point of linestring with given point. Index is 0-based. Negative index are counted backwards, e.g., -1 is last point.

Format: ST_SetPoint (linestring: geometry, index: integer, point: geometry)

Example:

SELECT ST_SetPoint(ST_GeomFromText('LINESTRING (0 0, 0 1, 1 1)'), 2, ST_GeomFromText('POINT (1 0)')) AS geom

Result:

+--------------------------+
|geom                      |
+--------------------------+
|LINESTRING (0 0, 0 1, 1 0)|
+--------------------------+

ST_SetSRID

Introduction: Sets the spatial reference system identifier (SRID) of the geometry.

Format: ST_SetSRID (A:geometry, srid: Integer)

SQL example:

SELECT ST_SetSRID(polygondf.countyshape, 3021)
FROM polygondf

ST_ShiftLongitude

Introduction: Modifies longitude coordinates in geometries, shifting values between -180..0 degrees to 180..360 degrees and vice versa. This is useful for normalizing data across the International Date Line and standardizing coordinate ranges for visualization and spheroidal calculations.

Note

This function is only applicable to geometries that use lon/lat coordinate systems.

Format: ST_ShiftLongitude (geom: geometry)

Since: v1.6.0

SQL example:

SELECT ST_ShiftLongitude(ST_GeomFromText('LINESTRING(177 10, 179 10, -179 10, -177 10)'))

Output:

LINESTRING(177 10, 179 10, 181 10, 183 10)

ST_SimplifyPolygonHull

Introduction: This function computes a topology-preserving simplified hull, either outer or inner, for a polygonal geometry input. An outer hull fully encloses the original geometry, while an inner hull lies entirely within. The result maintains the same structure as the input, including handling of MultiPolygons and holes, represented as a polygonal geometry formed from a subset of vertices.

Vertex reduction is governed by the vertexFactor parameter ranging from 0 to 1, with lower values yielding simpler outputs with fewer vertices and reduced concavity. For both hull types, a vertexFactor of 1.0 returns the original geometry. Specifically, for outer hulls, 0.0 computes the convex hull; for inner hulls, 0.0 produces a triangular geometry.

The simplification algorithm iteratively removes concave corners containing the least area until reaching the target vertex count. It preserves topology by preventing edge crossings, ensuring the output is a valid polygonal geometry in all cases.

Format:

ST_SimplifyPolygonHull(geom: Geometry, vertexFactor: Double, isOuter: Boolean = true)

ST_SimplifyPolygonHull(geom: Geometry, vertexFactor: Double)

SQL Example

SELECT ST_SimplifyPolygonHull(
        ST_GeomFromText('POLYGON ((30 10, 40 40, 45 45, 50 30, 55 25, 60 50, 65 45, 70 30, 75 20, 80 25, 70 10, 30 10))'),
       0.4
)

Output:

POLYGON ((30 10, 40 40, 45 45, 60 50, 65 45, 80 25, 70 10, 30 10))

SQL Example

SELECT ST_SimplifyPolygonHull(
        ST_GeomFromText('POLYGON ((30 10, 40 40, 45 45, 50 30, 55 25, 60 50, 65 45, 70 30, 75 20, 80 25, 70 10, 30 10))'),
       0.4, false
)

Output:

POLYGON ((30 10, 70 10, 60 50, 55 25, 30 10))

ST_SimplifyPreserveTopology

Introduction: Simplifies a geometry and ensures that the result is a valid geometry having the same dimension and number of components as the input, and with the components having the same topological relationship.

Format: ST_SimplifyPreserveTopology (A:geometry, distanceTolerance: Double)

SELECT ST_SimplifyPreserveTopology(polygondf.countyshape, 10.0)
FROM polygondf

ST_SimplifyVW

Introduction: This function simplifies the input geometry by applying the Visvalingam-Whyatt algorithm.

Note

The simplification may not preserve topology, potentially producing invalid geometries. Use ST_SimplifyPreserveTopology to retain valid topology after simplification.

Format: ST_SimplifyVW(geom: Geometry, tolerance: Double)

SQL Example

SELECT ST_SimplifyVW(ST_GeomFromWKT('POLYGON((8 25, 28 22, 28 20, 15 11, 33 3, 56 30, 46 33,46 34, 47 44, 35 36, 45 33, 43 19, 29 21, 29 22,35 26, 24 39, 8 25))'), 80)

Output:

POLYGON ((8 25, 28 22, 15 11, 33 3, 56 30, 47 44, 43 19, 24 39, 8 25))

ST_Snap

Introduction: Snaps the vertices and segments of the input geometry to reference geometry within the specified tolerance distance. The tolerance parameter controls the maximum snap distance.

If the minimum distance between the geometries exceeds the tolerance, the input geometry is returned unmodified. Adjusting the tolerance value allows tuning which vertices should snap to the reference and which remain untouched.

Format: ST_Snap(input: Geometry, reference: Geometry, tolerance: double)

Input geometry:

SQL Example:

SELECT
    ST_Snap(poly, line, ST_Distance(poly, line) * 1.01) AS polySnapped FROM (
        SELECT ST_GeomFromWKT('POLYGON ((236877.58 -6.61, 236878.29 -8.35, 236879.98 -8.33, 236879.72 -7.63, 236880.35 -6.62, 236877.58 -6.61), (236878.45 -7.01, 236878.43 -7.52, 236879.29 -7.50, 236878.63 -7.22, 236878.76 -6.89, 236878.45 -7.01))') as poly,
            ST_GeomFromWKT('LINESTRING (236880.53 -8.22, 236881.15 -7.68, 236880.69 -6.81)') as line
)

Output:

POLYGON ((236877.58 -6.61, 236878.29 -8.35, 236879.98 -8.33, 236879.72 -7.63, 236880.69 -6.81, 236877.58 -6.61), (236878.45 -7.01, 236878.43 -7.52, 236879.29 -7.5, 236878.63 -7.22, 236878.76 -6.89, 236878.45 -7.01))

ST_Split

Introduction: Split an input geometry by another geometry (called the blade). Linear (LineString or MultiLineString) geometry can be split by a Point, MultiPoint, LineString, MultiLineString, Polygon, or MultiPolygon. Polygonal (Polygon or MultiPolygon) geometry can be split by a LineString, MultiLineString, Polygon, or MultiPolygon. In either case, when a polygonal blade is used then the boundary of the blade is what is actually split by. ST_Split will always return either a MultiLineString or MultiPolygon even if they only contain a single geometry. Homogeneous GeometryCollections are treated as a multi-geometry of the type it contains. For example, if a GeometryCollection of only Point geometries is passed as a blade it is the same as passing a MultiPoint of the same geometries.

Format: ST_Split (input: geometry, blade: geometry)

SQL Example:

SELECT ST_Split(
    ST_GeomFromWKT('LINESTRING (0 0, 1.5 1.5, 2 2)'),
    ST_GeomFromWKT('MULTIPOINT (0.5 0.5, 1 1)'))

Output: MULTILINESTRING ((0 0, 0.5 0.5), (0.5 0.5, 1 1), (1 1, 1.5 1.5, 2 2))

ST_SRID

Introduction: Return the spatial reference system identifier (SRID) of the geometry.

Format: ST_SRID (A:geometry)

SQL example:

SELECT ST_SRID(polygondf.countyshape)
FROM polygondf

ST_StartPoint

Introduction: Returns first point of given linestring.

Format: ST_StartPoint(geom: geometry)

SQL example:

SELECT ST_StartPoint(ST_GeomFromText('LINESTRING(100 150,50 60, 70 80, 160 170)'))

Output: POINT(100 150)

ST_SubDivide

Introduction: Returns a multi-geometry divided based of given maximum number of vertices.

Format: ST_SubDivide(geom: geometry, maxVertices: int)

SQL example:

SELECT Sedona.ST_AsText(Sedona.ST_SubDivide(Sedona.ST_GeomFromText('LINESTRING(0 0, 85 85, 100 100, 120 120, 21 21, 10 10, 5 5)'), 5));

Output:

MULTILINESTRING ((0 0, 5 5), (5 5, 10 10), (10 10, 21 21), (21 21, 60 60), (60 60, 85 85), (85 85, 100 100), (100 100, 120 120))

ST_SubDivideExplode

Introduction: It works the same as ST_SubDivide but returns new rows with geometries instead of a multi-geometry.

Format: SELECT SEDONA.ST_AsText(GEOM) FROM table(SEDONA.ST_SubDivideExplode(geom: geometry, maxVertices: int))

Example:

Query:

SELECT Sedona.ST_AsText(GEOM)
FROM table(Sedona.ST_SubDivideExplode(Sedona.ST_GeomFromText('LINESTRING(0 0, 85 85, 100 100, 120 120, 21 21, 10 10, 5 5)'), 5));

Result:

+-----------------------------+
|geom                         |
+-----------------------------+
|LINESTRING(0 0, 5 5)         |
|LINESTRING(5 5, 10 10)       |
|LINESTRING(10 10, 21 21)     |
|LINESTRING(21 21, 60 60)     |
|LINESTRING(60 60, 85 85)     |
|LINESTRING(85 85, 100 100)   |
|LINESTRING(100 100, 120 120) |
+-----------------------------+

ST_SymDifference

Introduction: Return the symmetrical difference between geometry A and B (return parts of geometries which are in either of the sets, but not in their intersection)

Format: ST_SymDifference (A:geometry, B:geometry)

Example:

SELECT ST_SymDifference(ST_GeomFromWKT('POLYGON ((-3 -3, 3 -3, 3 3, -3 3, -3 -3))'), ST_GeomFromWKT('POLYGON ((-2 -3, 4 -3, 4 3, -2 3, -2 -3))'))

Result:

MULTIPOLYGON (((-2 -3, -3 -3, -3 3, -2 3, -2 -3)), ((3 -3, 3 3, 4 3, 4 -3, 3 -3)))

ST_Transform

Introduction:

Transform the Spatial Reference System / Coordinate Reference System of A, from SourceCRS to TargetCRS. For SourceCRS and TargetCRS, WKT format is also available.

Note

By default, this function uses lat/lon order. You can use ST_FlipCoordinates to swap X and Y.

Note

If ST_Transform throws an Exception called "Bursa wolf parameters required", you need to disable the error notification in ST_Transform. You can append a boolean value at the end.

Format: ST_Transform (A:geometry, SourceCRS:string, TargetCRS:string ,[Optional] DisableError)

SQL example (simple):

SELECT ST_Transform(polygondf.countyshape, 'epsg:4326','epsg:3857')
FROM polygondf

SQL example (with optional parameters):

SELECT ST_Transform(polygondf.countyshape, 'epsg:4326','epsg:3857', false)
FROM polygondf

Note

The detailed EPSG information can be searched on EPSG.io.

ST_Translate

Introduction: Returns the input geometry with its X, Y and Z coordinates (if present in the geometry) translated by deltaX, deltaY and deltaZ (if specified)

If the geometry is 2D, and a deltaZ parameter is specified, no change is done to the Z coordinate of the geometry and the resultant geometry is also 2D.

If the geometry is empty, no change is done to it. If the given geometry contains sub-geometries (GEOMETRY COLLECTION, MULTI POLYGON/LINE/POINT), all underlying geometries are individually translated.

Format: ST_Translate(geometry: geometry, deltaX: deltaX, deltaY: deltaY, deltaZ: deltaZ)

Example:

Input: ST_Translate(GEOMETRYCOLLECTION(MULTIPOLYGON (((1 0, 1 1, 2 1, 2 0, 1 0)), ((1 2, 3 4, 3 5, 1 2))), POINT(1, 1, 1), LINESTRING EMPTY), 2, 2, 3)

Output: GEOMETRYCOLLECTION(MULTIPOLYGON (((3 2, 3 3, 4 3, 4 2, 3 2)), ((3 4, 5 6, 5 7, 3 4))), POINT(3, 3, 4), LINESTRING EMPTY)

Input: ST_Translate(POINT(1, 3, 2), 1, 2)

Output: POINT(2, 5, 2)

ST_TriangulatePolygon

Introduction: Generates the constrained Delaunay triangulation for the input Polygon. The constrained Delaunay triangulation is a set of triangles created from the Polygon's vertices that covers the Polygon area precisely, while maximizing the combined interior angles across all triangles compared to other possible triangulations. This produces the highest quality triangulation representation of the Polygon geometry. The function returns a GeometryCollection of Polygon geometries comprising this optimized constrained Delaunay triangulation. Polygons with holes and MultiPolygon types are supported. For any other geometry type provided, such as Point, LineString, etc., an empty GeometryCollection will be returned.

Format: ST_TriangulatePolygon(geom: Geometry)

SQL Example

SELECT ST_TriangulatePolygon(
        ST_GeomFromWKT('POLYGON ((0 0, 10 0, 10 10, 0 10, 0 0), (5 5, 5 8, 8 8, 8 5, 5 5))')
    )

Output:

GEOMETRYCOLLECTION (POLYGON ((0 0, 0 10, 5 5, 0 0)), POLYGON ((5 8, 5 5, 0 10, 5 8)), POLYGON ((10 0, 0 0, 5 5, 10 0)), POLYGON ((10 10, 5 8, 0 10, 10 10)), POLYGON ((10 0, 5 5, 8 5, 10 0)), POLYGON ((5 8, 10 10, 8 8, 5 8)), POLYGON ((10 10, 10 0, 8 5, 10 10)), POLYGON ((8 5, 8 8, 10 10, 8 5)))

ST_UnaryUnion

Introduction: This variant of ST_Union operates on a single geometry input. The input geometry can be a simple Geometry type, a MultiGeometry, or a GeometryCollection. The function calculates the geometric union across all components and elements within the provided geometry object.

Format: ST_UnaryUnion(geometry: Geometry)

SQL Example

SELECT ST_UnaryUnion(ST_GeomFromWKT('MULTIPOLYGON(((0 10,0 30,20 30,20 10,0 10)),((10 0,10 20,30 20,30 0,10 0)))'))

Output:

POLYGON ((10 0, 10 10, 0 10, 0 30, 20 30, 20 20, 30 20, 30 0, 10 0))

ST_Union

Introduction: Return the union of geometry A and B

Format: ST_Union (A:geometry, B:geometry)

Example:

SELECT ST_Union(ST_GeomFromWKT('POLYGON ((-3 -3, 3 -3, 3 3, -3 3, -3 -3))'), ST_GeomFromWKT('POLYGON ((1 -2, 5 0, 1 2, 1 -2))'))

Result:

POLYGON ((3 -1, 3 -3, -3 -3, -3 3, 3 3, 3 1, 5 0, 3 -1))

ST_VoronoiPolygons

Introduction: Returns a two-dimensional Voronoi diagram from the vertices of the supplied geometry. The result is a GeometryCollection of Polygons that covers an envelope larger than the extent of the input vertices. Returns null if input geometry is null. Returns an empty geometry collection if the input geometry contains only one vertex. Returns an empty geometry collection if the extend_to envelope has zero area.

Format: ST_VoronoiPolygons(g1: Geometry, tolerance: Double, extend_to: Geometry)

Optional parameters:

tolerance : The distance within which vertices will be considered equivalent. Robustness of the algorithm can be improved by supplying a nonzero tolerance distance. (default = 0.0)

extend_to : If a geometry is supplied as the "extend_to" parameter, the diagram will be extended to cover the envelope of the "extend_to" geometry, unless that envelope is smaller than the default envelope (default = NULL. By default, we extend the bounding box of the diagram by the max between bounding box's height and bounding box's width).

SQL Example:

SELECT st_astext(ST_VoronoiPolygons(ST_GeomFromText('MULTIPOINT ((0 0), (1 1))')));

Output:

GEOMETRYCOLLECTION(POLYGON((-1 2,2 -1,-1 -1,-1 2)),POLYGON((-1 2,2 2,2 -1,-1 2)))

ST_X

Introduction: Returns X Coordinate of given Point null otherwise.

Format: ST_X(pointA: Point)

SQL example:

SELECT ST_X(ST_POINT(0.0 25.0))

Output: 0.0

ST_XMax

Introduction: Returns the maximum X coordinate of a geometry

Format: ST_XMax (A:geometry)

Example:

SELECT ST_XMax(df.geometry) AS xmax
FROM df

Input: POLYGON ((-1 -11, 0 10, 1 11, 2 12, -1 -11))

Output: 2

ST_XMin

Introduction: Returns the minimum X coordinate of a geometry

Format: ST_XMin (A:geometry)

Example:

SELECT ST_XMin(df.geometry) AS xmin
FROM df

Input: POLYGON ((-1 -11, 0 10, 1 11, 2 12, -1 -11))

Output: -1

ST_Y

Introduction: Returns Y Coordinate of given Point, null otherwise.

Format: ST_Y(pointA: Point)

SQL example:

SELECT ST_Y(ST_POINT(0.0 25.0))

Output: 25.0

ST_YMax

Introduction: Return the minimum Y coordinate of A

Format: ST_YMax (A:geometry)

SQL example:

SELECT ST_YMax(ST_GeomFromText('POLYGON((0 0 1, 1 1 1, 1 2 1, 1 1 1, 0 0 1))'))

Output: 2

ST_YMin

Introduction: Return the minimum Y coordinate of A

Format: ST_Y_Min (A:geometry)

SQL example:

SELECT ST_YMin(ST_GeomFromText('POLYGON((0 0 1, 1 1 1, 1 2 1, 1 1 1, 0 0 1))'))

Output : 0

ST_Z

Introduction: Returns Z Coordinate of given Point, null otherwise.

Format: ST_Z(pointA: Point)

SQL example:

SELECT ST_Z(ST_POINT(0.0 25.0 11.0))

Output: 11.0

ST_ZMax

Introduction: Returns Z maxima of the given geometry or null if there is no Z coordinate.

Format: ST_ZMax(geom: geometry)

SQL example:

SELECT ST_ZMax(ST_GeomFromText('POLYGON((0 0 1, 1 1 1, 1 2 1, 1 1 1, 0 0 1))'))

Output: 1.0

ST_ZMin

Introduction: Returns Z minima of the given geometry or null if there is no Z coordinate.

Format: ST_ZMin(geom: geometry)

SQL example:

SELECT ST_ZMin(ST_GeomFromText('LINESTRING(1 3 4, 5 6 7)'))

Output: 4.0